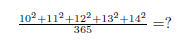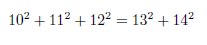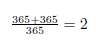代数の秘密

前回の記事は良い反応を示しました（ありがとう）。 だから今日は「忘れられた数学」の世界から何かを楽しんでください！   

算術は、漠然とした手段でその拠点のいくつかを証明できないことがよくあります。 これらの場合、より一般的な代数法が必要です。 代数的に正当化されるこれらのタイプの算術定理には、省略された算術演算に関する多くの規則があります。

スピード乗算:

コンピューターや電卓がなかった昔、偉大な算術学者は多くの単純な代数的トリックを使用していました。 あなたの人生を楽にするために：

「x」は乗算を表します（LaTeXを試すのが面倒でした:-)）

を見ようよ：

 988²=？

頭の中で解決できますか？

とても簡単です。詳しく見てみましょう。


988 x 988 =（988 + 12）x（998 -12）+12²= 1000 x 976 + 144 = 976 144

ここで何が起こっているのかを理解するのも簡単です。

（a + b）（a --b）+b²=a²--b²+b²=a²

これまでのところOKです。 それでは、数学をすばやく実行してみましょう-次のような組み合わせでも

986 x 997、電卓なし！

986 x 997 =（986-3）x 1000 + 3 x 14 = 983 042

ここで何が起こったのですか？ 次のように要因を書き留めることができます。

続きを読みます