ジャニベコフ効果
今日、好奇心旺盛な人のための物理学の分野からの何か: ジャニベコフ効果テニスラケットの定理としても知られているは、XNUMXつの異なる慣性モーメントを持つ回転体の不安定性を説明しています。 慣性モーメントは、回転運動の変化に対する物体の抵抗を示します。 それは特定の回転軸と形状に依存します。 古典的なハミルトン系のダイナミクスを理解することは、数学的な記述をはるかに超える多数のアプリケーションにとって、依然として重要な目標です。 自由度が少ない可積分系の場合、効率的なアプローチは、機械システムの動的特性を特徴付ける幾何学的分析に基づいています。 このような幾何学的現象は、通常、実験的に観察できる特定の効果のロバスト性の起源です。 それらのXNUMXつはいわゆるです。 ジャニベコフ効果 またはテニスラケット効果とも呼ばれます。
ISSの無重力状態におけるジャニベコフ効果
この現象の優れた詳細な理論的導出は、ここ(https://arxiv.org/pdf/1606.08237.pdf)にあります。 ここでは、少し荒いが、それでも現象を説明している人を扱っています。 残念ながら、ここでは剛体のダイナミクスに関する事前の知識が必要です。
I1が最小で、I2が最大になるような、慣性モーメントI3、I1、およびI3を持つ(対角化された)慣性行列を考えます。 ここで、主慣性モーメントI3の軸の周りの動きを考えます。 角速度ベクトルは次のとおりです。
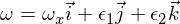
ここで、エプシロンは他のXNUMXつの主軸の小さな摂動です。 これをオイラー方程式に挿入すると、次のようになります。
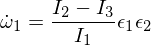
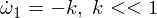
ここで、XNUMX番目のオイラー方程式を微分します。
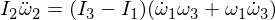
私たちの表現でオメガ1とオメガ3を置き換えると、エプシロンを乗算すると無視できるほど小さくなります。
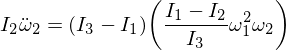
これにより、次の形式のオメガ2の微分方程式が得られます。
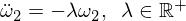
基本的な解決策は次のとおりです。
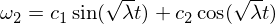
したがって、オメガ1軸の回転障害は安定しており、周期的な動きをするか、剛体運動の用語では歳差運動をすることがわかっています。 オメガ3障害は、上記と同様の議論に従います。それを解決するための演習として残しておきます。 中間軸には次のものがあります。
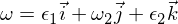
オイラー方程式に挿入:
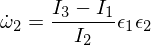
XNUMX番目のオイラー方程式を微分すると次のようになります。
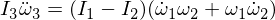
派生した式を置き換えましょう:
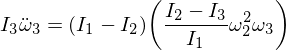
次に、次の微分方程式を並べ替えて導出します。
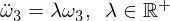
係数が正になっていることに注意してください。これにより、指数解が得られます。
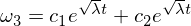
この解決策は、オメガ3が中間軸に沿って不安定であり、オメガ2の乱れがあることを示しています。
これは何を意味するのでしょうか?
これで、定理を理解するために導き出し、学んだすべてを組み合わせることができます。 簡単に言えば、中間軸に沿った回転が妨げられると、指数解を伴う微分方程式が得られます。 これは、他のXNUMXつの軸で観察される正確な動きとは対照的に、不安定な動きにつながります。 この結果は非常に驚くべきものです。 中間慣性モーメントが不安定な回転をもたらす理由を想像できないため、このような定理を直感的にサポートすることはできません。 それは本質的に純粋に数学的なもののようです。